インフォメーション・テクノロジーから
インフォメーション・バリュー・テクノロジーへ
インフォメーション・バリュー・テクノロジーへ
|
|
|
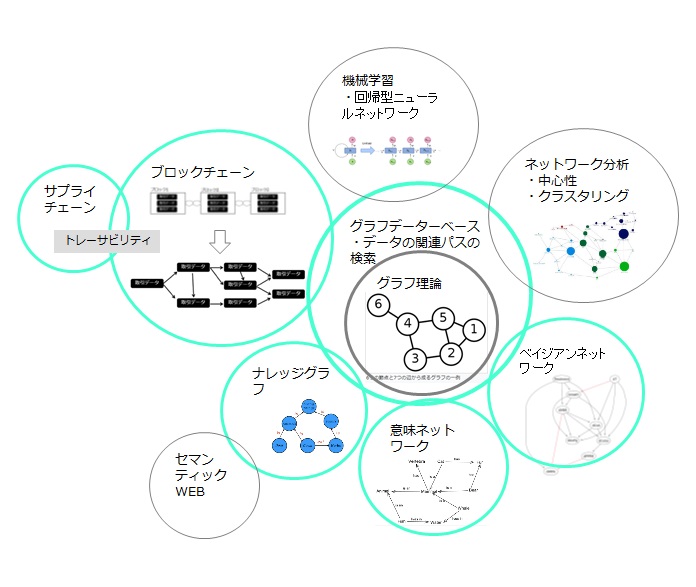
グラフはノードとエッジから成っており、グラフ・データベースはノード・データとエッジ・データ(リンク・データ)から成っています。ノード・データは 従来のリスト型データベースであり、リスト型データベースのテーブル間の関連を定義できるデータベースがRDBです。それが、さらに進化したものが オブジェクト・データベース(ODB)で従来のRDBと異なるのはインヘリタンス(データのリンク)がRDBに比べてより自由に定義できることにあります。 RDBはデータの関係性に関連する操作は複数のルックアップテーブルを必要とします。グラフ・データベースは、関連を表すモデリングにおいてはるかに 効率的です。複雑なデータ相互接続を伴う問題の処理のパフォーマンスが大幅に向上します。 |
|
|
|
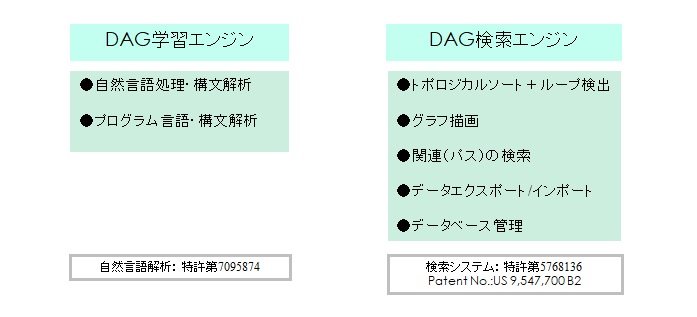
一般的なグラフ理論は無向巡回グラフを基礎としています。ただし、一般的なアルゴリズムで解を求めようとするとNP問題となります。多くの問題は 無向巡回グラフを有向非巡回グラフ(DAG:Directed Acyclic Graph)に変換(トポロジカルソート)することで解(近似解)を求めることが出来ます。 近似解となる一つの要因はトポロジカルソートの時点でループが発見された場合の処理になります。例えば、一般的な道路網は両側通行のできる道を含んでいて 一廻りすると元の地点に戻ってきます。これはグラフで分類すると無向巡回グラフになりますから、A地点からB地点までのルートは数多く存在しますが、 命題がA地点からB地点までの最短のルートを求めることである場合は、道路網をトポロジカルソートして有向非巡回グラフにすれば解を求めることができます。 |
|
|
|
グラフ・データベース検索は、ノードの検索に加えてエッジ(リンク)のパス(ルート)の検索を効率よく行えることが大きなメリットとなります。 パスの検索はグラフ理論に基づく様々なアルゴリズムが存在します。例えば、サプライチェーンの問題で複数のエンティティを検索キーとして、それらに同時に 関連する供給パスを得ようとするような場合に効率良く解を求めることが出来ます。さらにDAG型のグラフデータベースへ置き換えることによって、ブロックチェーンの いくつかの問題点を解決することができるようになってきています。 |
|
|
|
リンク予測は、グラフの構造情報からノード間のミッシングリンクの存在を予測したり、誤ったリンクを特定したり、グラフ・ネットワークの進化メカニズムの評価などに 役立ちます。グラフにエッジ(リンク)を追加することで、より期待される結果を得ることが出来れば、ミッシングリンクが発見されたことになります。 リンク予測のアルゴリズムには、トポロジカルな手法と非トポロジカルな手法があります。トポロジカルな手法は、グラフの形状や接続性だけに基づいてリンク予測を 行います。例えば、グラフ・データベース検索で検索開始→結果およびその逆の双方向から確率の最大となるパスの組み合わせを探すことよってミッシングリンクの候補を 見つける方法などです。非トポロジカルな手法は、ノードやリンクに付随する属性やメタデータなど、ネットワーク以外の情報も利用し、属性やメタデータの類似性に 基づいてユークリッド距離、余弦相似などのアルゴリズムを用いてリンクの存在を予測します。 リンク予測の例には、ソーシャルネットワーク内のユーザー間の友達リンクの予測、引用ネットワーク内の共著リンクの予測、生物学的ネットワーク内の遺伝子と タンパク質間の相互作用の予測などが含まれます。電子商取引では、ユーザーにアイテムを推奨するために使用します。引用データベースのキュレーションでは、 レコードの重複排除に使用できます。バイオ・インフォマティクスでは、タンパク質間相互作用(PPI)の予測に使用されています。また、セキュリティ関連の アプリケーションではテロリストや犯罪者の隠れたグループを識別するためにも使用されます。リンク予測は、時間的な側面を持つこともできます。 |